Legutóbbi leckénkben végre valahára munkára fogtuk a CSS3 egyik leglátványosabb újdonságát, a 3D transzformációt, ez alkalommal pedig megnézzük, hogy – némi számolgatást követően – hogyan lesz a kockából hengerpalást, de még előtte „megrajzoljuk” a Windows 8 logóját, és egy kicsit ismét eljátszogatunk a betűkkel, ahogyan az „képes előzetesként” már látható volt a múlt hónapban is. A leckéhez tartozó példaprogram letölthető a weboldalunkról.
Windows 8 logó CSS3 módra
Futólag megnézve a Windows 8 logóját azt mondhatnánk, hogy két részből áll: a stilizált ablakból (vagy csempékből) és a szövegből. De ha kicsit alaposabban és főként mint megszerkesztésre váró feladatot vizsgáljuk meg a képet, azt mondhatjuk, hogy 3+1 elemre lesz szükségünk.
Annak érdekében, hogy szépen középre tudjuk igazítani az egész logót, szükségünk lesz egy „csomagoló” [ccei]<div>[/ccei]-re ([ccei]<div class="wrapper">[/ccei]), amin belül egy kis játék miatt még egy plusz [ccei]<div>[/ccei]-et hozunk létre ([ccei]<div id="win8logo">[/ccei]). (Elvileg e két célra használhatnánk egyetlen [ccei]<div>[/ccei]-et is, de ennyi „divitis” talán még belefér a kényes ízlésűeknek is.) Ez utóbbi [ccei]<div>[/ccei]-en belül helyezzük el a három [ccei]<span>[/ccei] elemünket: egyet az ablaknak, egyet a trademark jelnek és egyet a Windows 8 szövegnek, amin belül +1-ként, „külön becsomagoljuk” a registered trademark jelet. A két speciális karakternek szerencsére van úgynevezett HTML entitása, így előbbit oldalunk kódjában[ccei] ™[/ccei]-ként, utóbbit pedig [ccei]®[/ccei]-ként írjuk.
Ezen kívül még a formázás előtt be kell szereznünk a Segoe betűkészlet közepesen kövér, más néven semibold változatát, ugyanis a Windows 8 szöveget majd ezzel kell írnunk. Éppen ezért CSS-ünk (windows8.css) azzal kezdődik, hogy – ahogyan ezt közel két éve, a Websuli 26. leckéjében tanultuk – új betűtípusként létrehozzuk a logóban használatos Segoe-t (1–4. sorok).
A win8logo azonosítóval ellátott [ccei]<div>[/ccei] – ami tulajdonképpen maga a teljes logó lesz – méretei közül csak a magasságot kell megadnunk, hiszen a szélességet majd kiadja a tényleges tartalom. De ezen kívül a legegyszerűbb már itt beállítanunk a betűtípust, -stílust, –méretet és -színt, sőt a betűközön is csökkentenünk kell egy kicsit, hiszen az eredeti logóban is sűrítettek a szövegen, valamint a TM karakter egyszerűbb pozicionálhatósága miatt beállítunk egy relatív pozicionálást is (16–24. sorok).
És most jön a lényeg, ami miatt a Websuliban is helyett kapott ez a logó: az ablak. A[ccei] <span>[/ccei]-t sorszintű elemről „lebegtetett”, relatívan pozicionált, blokkszintű elemmé alakítjuk, majd megadjuk a méreteit, a szövegszínt itt háttérszínnek is beállítjuk (27–32. sorok). Kisebb logikai ugrással még mielőtt beforgatnánk az ablakot, létrehozzuk a függőleges és vízszintes osztásokat. Ezekhez két pszeudó elemet fogunk használni, amelyet a böngészővel – elvileg – a[ccei] <span>[/ccei] elé (:before) és mögé (:after) illesztetünk be. Közös mindkettőben, hogy a pozíciójukat abszolút módon fogjuk megadni, a tartalmuk nem, de sima fehér keretük lesz (41–46. sorok). Ám míg előbbi magassága 100 százalék, szélessége nulla, vízszintesen középre igazított, valamint bal és jobb oldali keretének 4-4 pixel vastagsága (48–53. sorok) van, addig utóbbinál pont fordítva lesz mindez (55–50. sorok).
Miután megvagyunk az ablak fehér vonalaival, jöhet az elforgatása. Ehhez a nézőpontot mindössze 250 pixellel hátrébb visszük, és az Y tengely körül forgatjuk el a [ccei]<span>[/ccei]-t -25 fokkal (34–38. sorok). Innentől kezdve szinte már rutinmunka, esetleg némi kísérletezgetéssel fűszerezve, hogy a két speciális karaktert a lehető legpontosabban helyezzük el (62–73. sorok).
Mint azt ígértük, a logót körbevevő [ccei]<div>[/ccei]-re egy kis játék miatt van szükségünk. Ez a játék pedig nem más, mint hogy beállítjuk, a logóban lévő ablak „hintázzon”, amíg az egér a logó fölött áll. Ehhez a CSS3 egy eddig nem használt modulját, az animációs modult fogjuk használni, méghozzá két lépésben. Először is megadjuk, hogy ha a logó bármely pontja fölé ér az egér, akkor az abban lévő ablakelemhez hozzárendelünk egy animációt. Ennek az animációnak meg kell mondanunk a nevét (window_anim), azt, hogy meddig tartson (2s), milyen ütemezéssel történjen a mozgás (linear), és hogy hányszor kell lejátszani az adott animációt (infinite – vagyis végtelen számú ismétlés) – és persze ahány böngésző, annyiféleképpen kell mindezeket megmondanunk (75–81. sorok), ahogyan az animáció kulcskockáinak beállítását is minden egyes böngészőnek külön-külön kell elmagyarázunk (83–112. sorok). Esetünkben az egyes időpontokhoz „csak” eltérő elforgatást állítunk be, hogy a kis ablak oda-vissza 10-10 fokkal forduljon el – de későbbi leckéinkben ennél kicsit összetettebb mozgásokra is használni fogjuk a CSS3 animációs modulját.
Betűlapozó
Három hónappal ezelőtt készítettünk két látványos címfeliratot a CSS3 transzformációk és egy rövid JavaScript programocska segítségével. Oldalunk korábbi kódján csak annyit változtatunk, hogy a címsorhoz hozzáadnunk egy azonosítót, ám JavaScriptünkhöz kicsit alaposabban hozzá kellett nyúlnunk.
Az új program ugyanis már nemcsak annyit tud, hogy a címsor egyes betűit [ccei]<span>[/ccei]-okba csomagolja (bár ez az alapértelmezett működése), hanem sokkal összetettebb struktúrákat is létre tudunk hozni segítségével, ahogyan az példánkban is látszik (cutletters.js). Kis programunk minden egyes betűhöz a következő struktúrát építi fel:
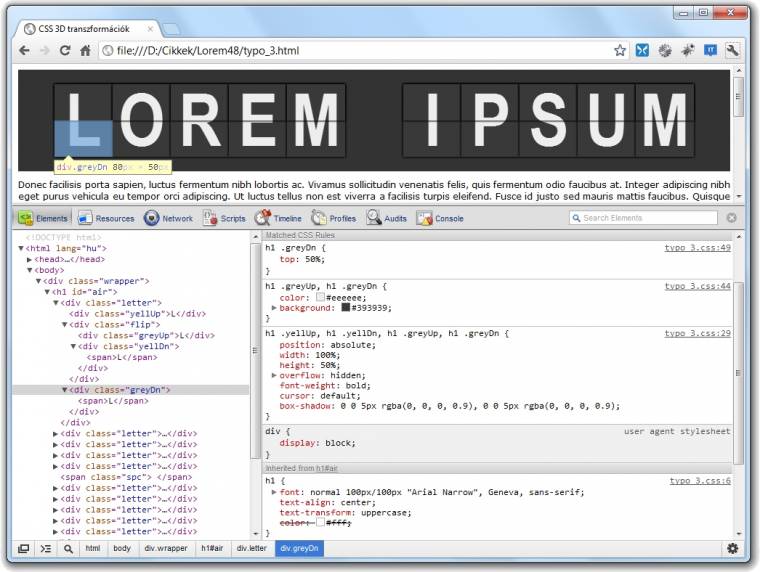
[cce] <div class="letter"> <div class="yellUp">L</div> <div class="flip"> <div class="greyUp">L</div> <div class="yellDn"><span>L</span></div> </div> <div class="greyDn"><span>L</span></div> </div> [/cce]
E kissé összetettnek tűnő felépítésre azért van szükségünk, mert minden egyes betűből két variáció készül, egy sárga (yell) és egy szürke (grey), és mind a kettőt félbevágjuk (Up és Dn). Miután a magasságukat 50 százalékra állítjuk, és a kilógó részeket levágjuk (typo_3.css: 29–37. sorok), csak az alsó elemekhez kell egy-egy [ccei]<span>[/ccei]-t használnunk, amiknek a margóját átállítva érjük el azt, hogy ne a betűk teteje, hanem az alja látszódjon (53–56. sorok). Mindezeken túl még a háttérszínekkel és a dobozok árnyékaival kell játszanunk egy kicsit, hogy a két-két darabból álló betűk úgy nézzenek ki, mint a régi reptéri vagy pályaudvari tájékoztató táblák betűi.
A fenti struktúrát megnézve jól látszik, hogy a szürke betű tetejét (greyUp) és a sárga betű alját (yellDn) egy lapra „ragasztottuk fel” (flip) úgy, hogy a sárga részt az X tengely körül elforgattuk 180 fokkal (89–95. sorok). Amikor az egyes betűk fölé ér az egér, akkor magát a kártyát forgatjuk el 180 fokkal, így a sárga rész kerül felülre, a szürke pedig hátra (97–103. sorok). Ám természetesen ez esetben a kártyát nem a középpontja körül kell elforgatnunk, hiszen a lap hátoldalán a sárga betű alja van, ezért a transzformáció középpontját a kártya aljához állítjuk be (63–67. sorok), így az szépen a helyére fog befordulni. (Érdekes módon az effektus csak Chrome alatt működik tökéletesen.)
Körhinta CSS3 módra
Múlt hónapban megnéztük, hogy mi történik, ha a kártyalap két oldalát egy-egy virtuális drótdarabbal előrébb és hátrébb visszük a forgástengelyhez képest, majd ha ugyanezen a módon hat irányba helyezünk el egy-egy lapot. De mi van akkor, ha nem hat, hanem több vagy éppen kevesebb lapot-képet szeretnénk megmutatni?
Ilyen esetekre az egyik bevált módszer, ha az egyes lapokat hengerpaláston vagy másképpen egy körhintán (carussel) helyezzük el. Ha felülről néznénk meg egy ilyen összeállítást, akkor tulajdonképpen egy n oldalú szabályos sokszöget látnánk. Ismerjük a sokszög oldalainak számát, valamint az oldalak hosszát, ám ahhoz, hogy létre tudjuk hozni a 3D-s transzformációk segítségével, azt is tudnunk kell, hogy hány fokkal kell elforgatnunk az egyes elemeket, és mennyivel kell eltolnunk ezeket a középponthoz képest.
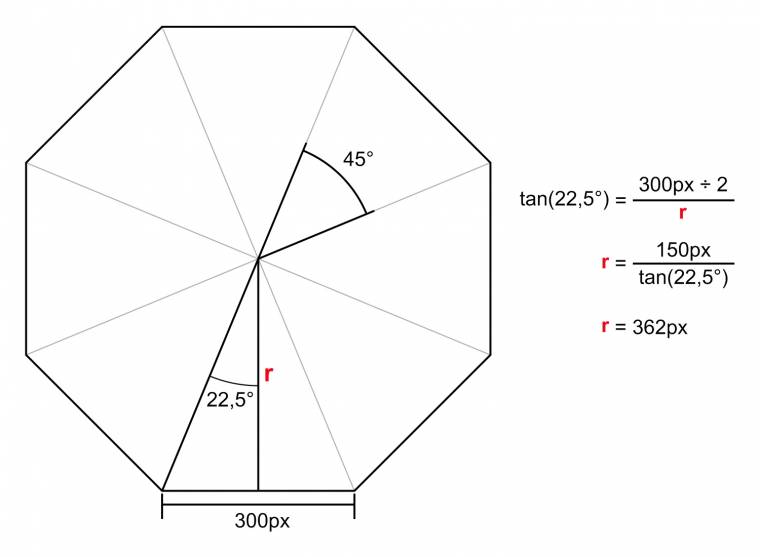
Előbbi kiszámítása nagyon egyszerű, hiszen mindössze el kell osztanunk a 360 fokot az oldalak számával, és máris tudjuk, hogy minden elemet ennyivel kell elforgatnunk az előzőhöz képest.
Az eltolás mértékét sem sokkal bonyolultabb kiszámolnunk, csak egy kis trigonometriára lesz szükségünk. Minden n oldalú szabályos sokszög feldarabolható n darab egyenlő oldalú háromszögre, amelyek 2-2 derékszögű háromszögre bonthatóak, amelyek egyik oldalának ismert a hossza (a lapok szélességének fele), és az oldallal szemközt lévő szög nagysága (360/n/2). Márpedig e szög tangense nem más, mint a vele szemközt lévő befogó (vagyis az ismert hossz) és mellette lévő befogó (vagyis a keresett távolság) hányadosa. Már csak át kell rendeznünk képletünket, és behelyettesítenünk az ismert értékeket, hogy megkapjuk a hiányzó távolságot.
Márpedig innentől kezdve nincs más dolgunk, mint létrehozni egy listát például nyolc elemmel (carousel.html: 14–25. sorok), beállítanunk az egyes elemek méretét és egyéb jellemzőit (carousel.css: 42–50. sorok), majd szépen egyesével beállítani az egyes listaelemek elforgatását az Y tengely körül és eltolását a Z tengely mentén (52–116. sorok). No meg persze azért ugyanennyivel hátrébb kell tolnunk az egész sokszöget, és megadnunk, hogy a listaelemek örököljék a szülőelem 3D-s terének beállításait (24–40. sorok).
Persze ez utóbbinak csak akkor van jelentősége, ha valamilyen trükkel, például egy kis JavaScript programmal mozgásra bírjuk az egész „körhintát”. De akkor már kényelemesebb, ha a HTML-ben csak egy üres listát hozunk létre (carousel2.html), és a CSS-ben is csak ennek beállításait végezzük el (carousel2.css), de magukat a listaelemeket már a JavaScript program (carousel2.js) hozza létre, amire ráadásul rábízhatjuk az elforgatási szögek és az eltolás kiszámítását is.
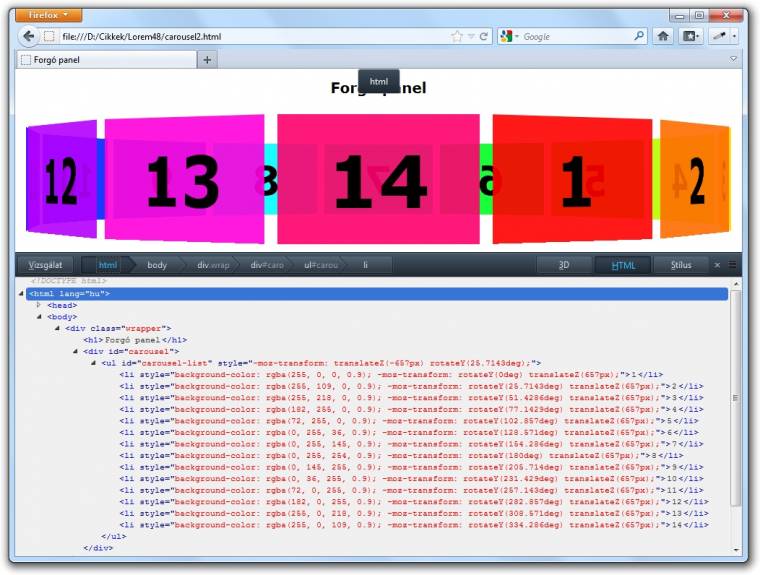
Ez esetben ugyanis csak az elemek számát kell nekünk megmondanunk (elemNum), minden mást rábízhatunk a programra. Gondot esetleg csak az okozhat, hogy minden böngészőben másként kell megadnunk a transzformálási stílust. Ám ezt Öveges tanár úr módszerét követve oldhatjuk meg a legegyszerűbben: végigpróbáljuk az összes lehetséges módot és reménykedünk, hogy legalább az egyik jó lesz (6–15. sorok).
Innentől kezdve már tényleg nagyon egyszerű a dolgunk, hiszen az oldalszélesség a rendelkezésünkre áll (a CSS-ben beállítottuk), a derékszögű háromszög ismert szögét radiánban nagyon egyszerűen meg tudjuk mondani (PI/elemNum), így az eltolás értéke már meg is van (18. sor), a listaelemeket létrehozó ciklusnak pedig teljesen mindegy, hogy kettő vagy kétszáz objektumot kell létrehoznia és transzformálnia – legfeljebb egy kicsit nagyobb lesz a listaelemek által létrehozott kör. Az pedig már csak rajtunk múlik, hogy ezen elemeket milyen tartalommal töltjük meg.