Miként azt a múlt hónapban is említettük, a kétdimenziós transzformációk moduljának munkaanyagát tavaly decemberben, egész pontosan december 15-én frissítették. Ami a mai leckénk szempontjából érdekesebb, hogy az eredeti változat 2009. december 1-jén került ki a W3C honlapjára – majdnem kilenc hónappal később, mint a háromdimenziós transzformációk modul jelenleg is aktuálisnak mondható munkaanyaga.
Pedig mind a két írást ugyanaz a három Apple szakember készítette, vagyis érdekes módon a három úriember, név szerint Dean Jackson, David Hyatt és Chris Marrin, jócskán hamarabb „tették le az asztalra” 3D-s ajánlásaikat, mint a 2D-seket. Ennek ellenére nem meglepő, hogy a böngészőgyártók előbb a 2D-s transzformációkat implementálták – így ezeket, ahogyan azt már a legutóbbi leckében is említettük, valamennyi úgynevezett modern böngészőben használhatjuk (leszámítva az Opera Mobile-t és Minit) –, és csak utána fogtak bele a 3D-s transzformációk fejlesztésébe.
Az sem véletlen, hogy mind a 2D-s, mind a 3D-s transzformációk területén a két webkites böngésző, és közülük is a nyílt forráskódú böngészőmotort fejlesztő Apple programja jár az élen. A 2D-s transzformációkat már 2008 márciusában – vagyis több mint egy évvel a munkaanyag publikálását megelőzően – megjelent Safari 3.1-ben használhattunk, míg a 3D-s transzformációk a 4.0-s Safariban debütáltak 2009. június elején. Ehhez képest a Google szinte napra pontosan két évvel később adta ki az első olyan Chrome verziót (a 12-es verziószámút 2011. június 7-én), amelyik már támogatta a 3D-s transzformációkat. A többi böngésző esetében van némi lemaradás, de úgy tűnik, hogy belátható időn belül mind az asztali, mind a mobil változatokba bekerül az elemek 3D-s transzformálhatósága.
Térbeli alakulások
A térbeli transzformációkat a síkbeliekhez hasonlóan a múlt havi leckénkben részletesen bemutatott transform stílustulajdonsággal tudjuk megadni. Mint azt említettük, ennek a stílustulajdonságnak az alapértelmezett értéke none, vagyis az oldalelemeken semmilyen transzformációt nem kell végrehajtaniuk a böngészőknek. Amennyiben szeretnénk valamely oldalelemet transzformálni, akkor úgynevezett transzformáló függvényeket kell használnunk. Egy transformon belül több ilyen transzformációs függvényt is megadhatunk, amelyek kumulálódnak, méghozzá – a későbbiek során ez még fontos lesz – a megadásuk sorrendjében.
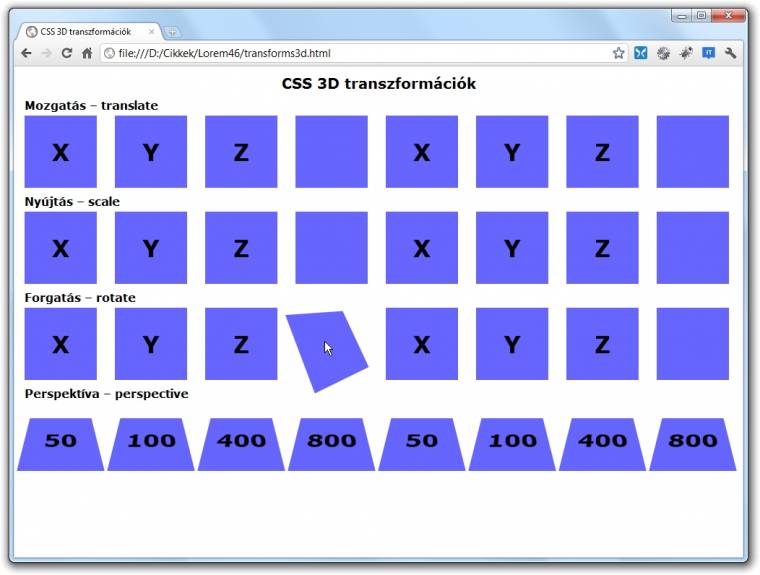
A múlt hónapban már részletesen átnéztük a tíz kétdimenziós transzformációs függvényt, éppen ezért ez alkalommal kizárólag az újabb dimenzióhoz kapcsolódó függvényeket szeretnénk bemutatni(a példaprogram letölthető az oldalunkról).
A translateX és translateY függvényekre természetesen ugyanúgy szükségünk lesz, amikor elemeinket szeretnénk vízszintesen vagy függőlegesen eltolni, sőt a translate-et is használhatjuk, ha csak e két koordinátatengellyel párhuzamosan akarjuk az elemeket elmozdítani. De abban az esetben, ha azt szeretnénk, hogy a kiválasztott elem a képernyő síkjára merőlegesen (is) elmozduljon, akkor a translateZ vagy a translate3d függvényeket kell használnunk.
Előbbinek természetesen csak egy távolság értéket kell megadnunk, míg utóbbinak – ellentétben a translate-nél leírtakkal – mind a három értékét be kell állítanunk, amelyek közül az első az X, a második Y, a harmadik pedig a Z irányú elmozdulás nagyságát adja meg.
Azt már korábbi stíluslapos tanulmányainkból tudjuk, hogy X irányban a pozitív elmozdulás mindig jobbra, Y irányban pedig lefelé történik (legalábbis, amíg el nem forgatjuk a koordinátatengelyt), az új, Z-tengelyről pedig azt kell tudnunk, hogy – alapértelmezés szerint – a pozitív irány a monitor síkjából kifelé mutat. Így ha a transform stílustulajdonságnak a translateZ(20px) értéket adjuk, akkor elemünk látszólag meg fog nőni, hiszen közelebb kerül hozzánk, míg a translateZ(-20px) hatására tőlünk távolodik, így mérete látszólag csökkenni fog.
Vízszintes és függőleges elmozdulásnál minden további nélkül megadhatjuk az elmozdulást százalékosan is, de arra nagyon oda kell figyelnünk, hogy amíg egy látható HTML elemnek biztosan van szélessége és magassága, amiből kiszámítható a kívánt elmozdulás, addig vastagsága (legalábbis még) nincs ezeknek az elemeknek, így a translateZ esetében a százalékosan megadott elmozdulás mindig nulla lesz.
Éppen ezek miatt a valószínűleg kizárólag a „jövőbeni fejlesztések számára fenntartott” okok miatt kerültek bele az ajánlásba a scaleZ és a scale3d transzformációs függvények, amelyekkel a nulla vastagságú elemek Z irányú kiterjedését tudjuk többszörözni. A scale3d-nek, hasonlóan a translate3d-hez és ellentétben a „sima” scale-lel meg kell adnunk mind a három paramétert – amelyekből a legutolsó tetszőleges érték lehet, hiszen a nullát teljesen mindegy, hogy mennyivel szorozzuk, az mindig nulla marad.
Érdekes módon amíg a munkaanyag összeállítói fontosnak érezték a scaleZ és scale3d transzformációs függvények bevezetését, addig a – legalábbis látszólag – fontosabbnak tűnő skewZ és skew3d függvények kimaradtak. Így az elemeket a böngészőkben dönteni a 3D-s transzformációs modul – jelenlegi formájában történő – implementálása esetén továbbra is csak az X és az Y tengelyekkel párhuzamosan tudjuk.
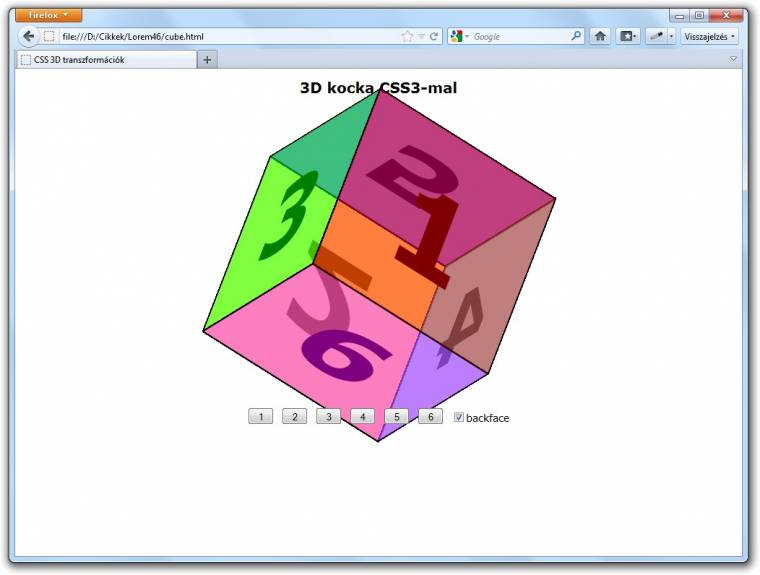
Némi túlzással mondhatnánk, hogy az eddig bemutatott transzformációs függvények esetében a „térbeliesítés” csak egy kis bővítés volt a 2D-s modul függvényeihez képest, ám ugyanezt már biztosan nem mondhatjuk el a rotate függvény kapcsán, már csak azért sem, mert amíg az eddigi egy függvényünkből hirtelen öt lesz. A rotate-et persze továbbra is használhatjuk az elemek síkbeli forgatására, ám leendő „nagyágyúink” a rotateX, a rotateY, a rotateZ és a rotate3d lesznek.
Az első három függvénynél elég egyértelmű a helyzet, hiszen mindegyik az adott tengely körül fordítja el a kiválasztott eleme(ke)t. A rotate3d azonban kicsit komplikáltabbnak tűnik, de szerencsére tényleg csak „tűnik”. A korábbiakból kiindulva azt várnánk, hogy ennek a transzformációs függvénynek is három paramétert kell megadnunk, amelyek közül az első az X, a második az Y, a harmadik pedig a Z tengely körüli elfordulást határozza meg. Ehelyett azonban három számot és egy szöget kell megadnunk, és az egyes elforgatási szögeket úgy kapjuk meg, hogy a megadott számokat egyesével megszorozzuk a negyedik paraméterként megadott szöggel. Így például ha a transform stílustulajdonságnak a rotate3d(.33, .5, .66, 90deg) értéket adjuk, akkor az – a kumulálódás miatti „torzulást” leszámítva – ugyanazt jelenti, mintha azt írtuk volna a kettőspont után, hogy rotateX(30deg), rotateY(45deg), rotateZ(60deg).
Természetesen a transzformációs függvények közül nem hiányozhat a matrix térbeli párja, a matrix3d sem. Ennek 16 paramétere – ahogy a munkaanyag fogalmaz – egy 3D-s transzformáció 4x4-es homogén mátrixát határozza meg, ám valószínűleg ezt a függvényt csak igen-igen kevesen fogják használni. Például a W3C oldalon található munkaanyagban a rotate3d függvénnyel ekvivalens matrix3d függvény kifejtése valamivel hosszabb, mint négy sor.
Fontos kiegészítők
Ahogyan a síkbeli transzformációknál, úgy a térbelieknél is sokszor fontos lehet, hogy melyik is az a pont, amihez képest történik az elmozdulás, elfordulás vagy éppen döntés. Ennek megadására ugyanúgy a transform-origin stílustulajdonságot használhatjuk, mint a 2D-s transzformációknál, azzal a nem elhanyagolható különbséggel, hogy itt három értéket adhatunk meg a megszokott módokon (pl. px, %, left, center bottom), és persze a százalékot itt sem használhatjuk a harmadik érték esetében.
Az összetettebb 3D-s elemcsoportok létrehozásakor nagyon fontos, hogy meg tudjuk adni, a beágyazott elemek miként viselkedjenek a térben. Az ezt meghatározó transform-style stílustulajdonságnak két értéket adhatunk meg. Az alapértelmezett flat azt jelenti, hogy az adott elemen belül található többi elemet a befoglaló elem „síkjára” vetített 2D-s képként kell megjeleníteni. Ezzel szemben a preserve-3d érték azt eredményezi, hogy a gyermek elemek megőrzik pozíciójukat a 3D-s térben, így nem véletlen, hogy az esetek többségében ezt a beállítást fogjuk használni.
A síkban ábrázolt képeket azért látjuk vagy inkább érezzük térbelinek, mert a szemlélőhöz közelebb eső elemek, elemrészek nagyobbnak, míg a távolabbiak kisebbnek látszanak, a távolodó párhuzamos vonalak pedig egymáshoz közelednek. Ezt idegen szóval perspektívának nevezzük. A 3D-s transzformációk esetében a perspektíve stílustulajdonság vagy az azonos nevű transzformációs függvény értékeként-paramétereként megadott számot érdemes úgy felfogni, mintha ezzel a nézőpont távolságát adnánk meg az elemektől.
Minél kisebb a perspektive értéke, annál közelebb vagyunk hozzájuk, így annál erősebb lesz a 3D-s hatás (mintha közelről egy széleslátószögű objektíven át néznénk), míg a nagyobb perspektíve érték, vagyis a nagyobb távolság csökkenti ezt a térbeliség érzetét (miként a teleobjektívek is csökkentik a térbeli távolságokat).
Ahogyan a transzformációknak megadhatjuk a „bázispontját”, úgy néha szükség lehet a perspektívahatás ún. „enyészpontjának”, vagyis annak a pontnak, ahol a párhuzamosok találkoznak a megváltoztatására. Alapértelmezés szerint ez a pont az elem középpontja, de a perspective-origin stílustulajdonsággal ezt bármikor megváltoztathatjuk.
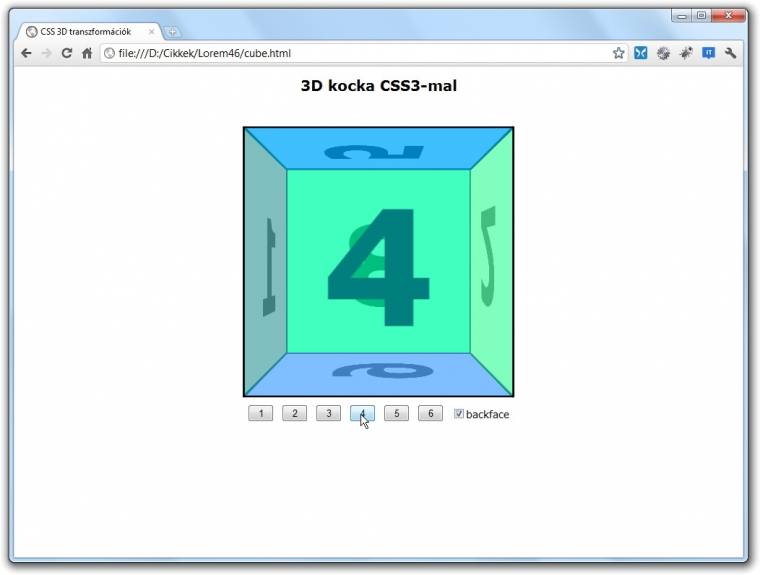
Legvégül kérdéses még, hogy mi legyen az egyes elemek, elemcsoportok „hátoldalával”, mit lássunk akkor, ha egy elemet elforgatunk akár az X, akár az Y tengellyel párhuzamosan 90 foknál nagyobb szögben. Beállításra használhatjuk a backface-visibility stílustulajdonságot. Ennek alapértelmezett értéke, a visible azt a hatást eredményezi, mintha elemünk egy átlátszó fóliára lenne rárajzolva, míg ezzel szemben a hiddennel azt adhatjuk meg, hogy elemünk mögé egy háttérszínű „karton” kerüljön.
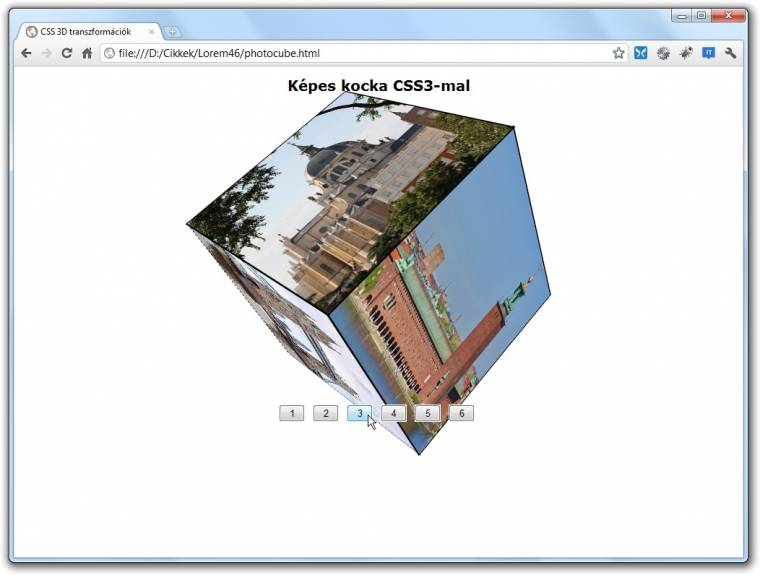
E kissé hosszúra nyúlt bevezető után a jövő hónapban elkezdjük munkára fogni a 3D-s transzformációkat. Megnézzük, ezen eszközök segítségével hogyan készíthetünk például képes kártyákat, kockákat, hogyan „dobhatjuk fel” oldalainkat.